【最优化】无约束优化方法-阻尼牛顿法

在上篇文章中，我介绍了无约束优化方法-牛顿法，见下：

最后我们说道了牛顿法的缺点，这里重新回顾一下，好引出阻尼牛顿法。

缺点：保证不了迭代方向是下降方向，这就是致命的！先看一个定理：

假设我们认可这个定理：直观理解见下：）

我们判断牛顿法的迭代方向是否朝着函数值下降的方向移动，也就是判断一下迭代方向和当前点的梯度值做内积，如果小于0就说明是下降方向，我们来计算一下：

迭代方向和当前点的梯度做内积为:

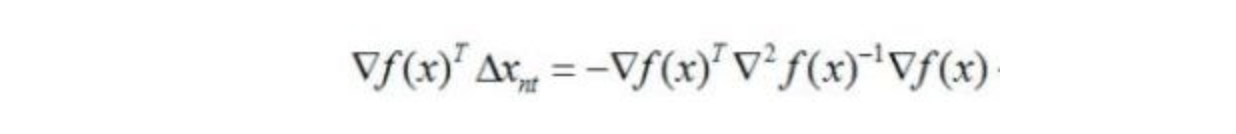
想让它小于0，也就是要求

大于0，这恰好是海塞矩阵正定的条件，也就是需要满足当前点的海塞矩阵是正定的，这个要求是很强的，因此并不能保证牛顿法的迭代方向是一定沿着函数值下降的方向。

为了解决这个问题，我们引入了阻尼牛顿法。

在前面说到的牛顿法缺点中，确定了迭代方向之后，迭代步长默认为1，但是这个迭代方向并不一定是朝着函数值下降的方向。

所以阻尼牛顿法为了解决这个问题，采取的做法是确定了迭代方向（和牛顿法一样的迭代方向）之后，还需要在该方向做一维搜索，寻找使得在该迭代方向上最优的迭代步长。公式如下：

阻尼牛顿法的算法步骤如下：

我们也给出牛顿法的算法步骤：

可以对比出，阻尼牛顿法与牛顿法的唯一差别就在于阻尼牛顿法在得到迭代方向之后，还在该方向进行了一维搜索，它能够保证每一次的迭代是朝着函数值下降的方向移动。

例如，本来牛顿法的迭代方向如果是沿着函数值上升的方向，那么在阻尼牛顿法中我的迭代步长变为负数即可。具体数值直接通过对步长求偏导数为0求解即可。

参考：